How To Find Volume Of A Cone With Height And Slant Height

In geometry, cone is a solid or hollow object with a round flat base and sides that slope up to a top point. The cone formulas, solved example & step by step calculations may useful for users to understand how the input values are being used in such calculations. Also this featured cone calculator uses the various conversion functions to find its area, volume & slant height in SI or metric or US customary units. A cone is an three-dimensional geometric shape having circular base and only one vertex. A cone can be formed by the locus of all straight line segments that join the vertex to the base has a rotational symmetry.

We can say that a cone have flat circular base and having one side curved surface. The volume and the total surface area of the cone depend upon the radius of base, height and slant height of the cone. To calculate the total surface area of a cone we need radius of circular base and height of cone. Then, it calculates the total surface area of cone using the formula given above and prints the result on screen using printf function.

In the field of geometry calculations, finding the area, volume & slanting height of a cone is very important to understand a part of basic mathematics. The volume of a cone can be defined as the amount of three dimensional space occupied by the right circular cone or the storage capacity of a right circular cone. Finding volume of a cone help us to solve many real life problems like, how much ice-cream is required to file an ice-cream cone. To calculate the volume of a right circular cone, we need radius of base height of cone. Volume of a cone is measured in cubic units like meter3, cm3 etc. Let's get right to it — we're here to calculate the surface area or volume of a right circular cone.

As you might already know, in a right circular cone, the height goes from the cone's vertex through the center of the circular base to form a right angle. Right circular cones are what we typically think of when we think of cones. A cone is a three dimensional geometric shape with one vertex and a circular base. The line form the centre of the base to the apex is the perpendicular height. Note- This problem can also be solved by using the formula of volume of cone in terms of height and slant height.

But that formula is a bit hard to remember and is not randomly used, so the method used here is the easiest one. Students must take extra care of units and must remember the Pythagoras theorem as it is commonly used in different types of problems. If a cone and cylinder have the same height and base radius, then the volume of cone is equal to one third of that of cylinder. That is, you would need the contents of three cones to fill up this cylinder. The same relationship holds for the volume of a pyramid and that of a prism .

In geometry, a cone is a 3-dimensional shape with a circular base and a curved surface that tapers from the base to the apex or vertex at the top. In simple words, a cone is a pyramid with a circular base. The slant height of a cone should not be confused with the height of a cone.

Slant height is the distance from the top of a cone, down the side to the edge of the circular base. Slant height is calculated as \(\sqrt\), where \(r\) represents the radius of the circular base, and \(h\) represents the height, or altitude, of the cone. Our traffic cone is a little different from the geometric shape called a cone. In geometry, the base of a cone is only a circle that does not extend beyond the opening of the cone.

The point of a cone in geometry is called the vertex point. The slant height and the altitude always meet at that vertex point in a cone. On the traffic cone, the two segments did not meet because the tip is flat and does not come to one point.

Let l be the slant height of the given frustum, a1 the apothem of the upper base, and a2 the apothem of the lower base. Using the formula for finding the measure of the apothem given below, solve for a1 and a2. The sum of the areas of the lateral faces of a frustum of a regular pyramid is the lateral surface area.

Since each lateral face is an isosceles trapezoid, then the area of each lateral face is one-half of the sum of the two edge bases multiplied by the slant height. In the equation below, b1 and b2 are the edges of the upper base and lower base of a frustum of a regular pyramid. In the equation below, P1 and P2 are the perimeters of the bases of the frustum. Lastly, the total surface area of the frustum is the sum of the lateral area and the areas of the two bases. B1 and B2 are the areas of the bases of the frustum.

Since the two bases of a frustum of a cone are circles, you can substitute πr2 to the variable B resulting in a more specific equation of the volume. Imagine two truncated cones with the same radius $r$ and a slant height of $h$ which is just a little less than $r$. The truncated cone can be very thin with a small upper base, or the walls can be almost vertical with the upper base having a radius just less than $r$. The two truncated cones agree on $r,h$ but not on volume. Imagine rotating the two trapezoids below to make truncated cones. The "height" of a cone, and the "slant height" of a cone are not the same thing.

The height of a cone is considered the vertical height or altitude of the cone. This is the perpendicular distance from the top of the cone down to the center of the circular base. The slant height of a cone is the distance from the top of the cone, down the side of the cone to the edge of the circular base. A cone folded flat forms a sector of a larger circle.Imagine a cone without its base, made out of paper. You then roll it out so it lies flat on a table.

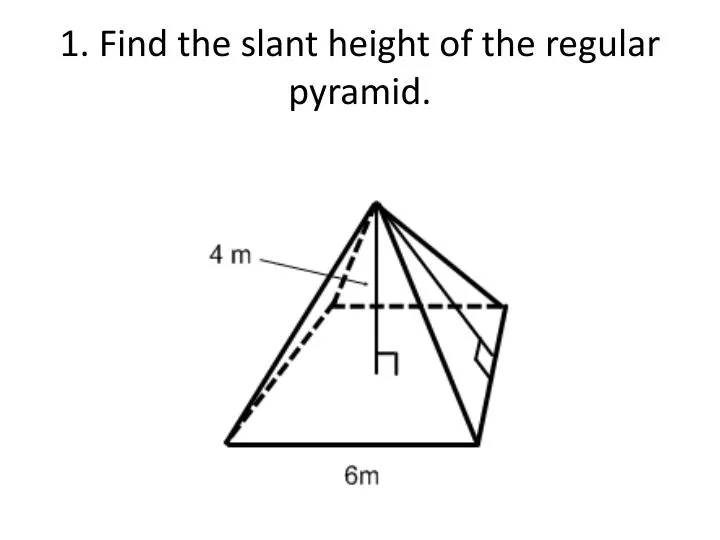
How To Find Cone Height With Slant Height You will get a shape like the one in the diagram above. It is a part of a larger circle, whose radius is equal to the slant height of the cone. The arc length of the sector is equivalent to the circumference of the cone base. In the video lesson, we learned how to find the slant height of a cone or pyramid when we know the altitude and information about the base. The same formula for slant height can be manipulated to find the altitude, the radius of the base , or half the side length of the base .

To calculate the slant height of either a cone or a pyramid, you need to imagine that you can look inside of the figure. First, we cut down through the cone from vertex point A to segment BC to get two halves. The cut surface of either half is now in the shape of an isosceles triangle, which is a triangle with two sides that are the same length. Those two sides were the slant height of the cone. We now have triangle ABC, where sides AB and AC have the same length. The distance along the outside of a cone, from the top to the base, is known as the slant height.

Given slant height, height and radius of a cone, we have to calculate the volume and surface area of the cone. In a cone, the perpendicular length between the vertex of a cone and the center of the circular base is known as the height of a cone. A cone's slanted lines are the length of a cone along the taper curved surface.

All of these parameters are mentioned in the figure above. And if you don't know any of the measurements of the shape, just use a ruler to measure the widest pie circular base and divide that number by 2 to get the radius. Let's say the radius of this cone's circular base is .5 inches (1.3 cm). If the cone is right circular the intersection of a plane with the lateral surface is a conic section. In general, however, the base may be any shape and the apex may lie anywhere . Contrasted with right cones are oblique cones, in which the axis passes through the centre of the base non-perpendicularly.

If the enclosed points are included in the base, the cone is a solid object; otherwise it is a two-dimensional object in three-dimensional space. The volume of a right circular cone is 52π ft3. Its altitude is 3 feet and the measure of its lower radius is three times the measure of its upper radius. In a frustum of a right circular cone, the diameter of the lower base is 24 feet, while the diameter of the upper base is 14 feet. If the slant height of the frustum is 13 feet, find the total area and the volume of the frustum.

The slant height of an object is the distance measured along a lateralface from the base to the apex along the "center" of the face. In other words, it is the altitude of the triangle comprising a lateral face (Kern and Bland 1948, p. 50). There is special formula for finding the volume of a cone. The volume is how much space takes up the inside of a cone. The answer to a volume question is always in cubic units.

The following mathematical formulas are used in this cone calculator to find the area, volume & slanting height of a cone. Identify the radius of the cone's base circle. If you have the diameter, cut it in half to get the radius. If you have the slant height and perpendicular height, use the Pythagorean theorem.

The base radius and slant height of a cone are 8 cm and `2 sqrtcm` respectively. A cone has a three-dimensional shape so calculating its volume can seem a little complicated. To help you understand better, in this article we explain what a cone is as well as how to calculate its volume. We detail the steps one by one and the formulas you have to use to calculate the volume of a cone with accurate examples.

Object, and surface area is, well, just that! It's the total area of the surface of a shape. Think of volume as the amount of liquid that you could fill an object with, and think of surface area as how much paper you could wrap over that object. Every cube, sphere, cylinder, cone , and so on has a volume and a surface area; and the formulas used for finding these measurements is different for each shape. The red segment DM measured 8 inches and that same segment is one side of the triangle.

The purple segment DY was the slant height of the pyramid, and it forms the hypotenuse of the triangle. DY is the length we are trying to calculate, so we will give it the variable c. Figures such as cones and pyramids have two measurements that indicate how tall the figure is.

One of these measurements is called the slant height and the other is called the altitude. In figure A is called vertex, AO is height, OC is radius, and AC is slant height of cone. The formula for the volume of a cone is (1/3)πr 2 h, where, "h" is the height of the cone, and "r" is the radius of the base.

Enter the height of the cone or the slant height of the cone, depending on which one is known. The height is the perpendicular distance between the cone tip and the center of the circular base. The slant height is the distance between the tip and the outside edge of the base. Enter a value for the radius of the circular base.

Remember that the radius is half of the diameter of a circle. You can choose different units of length, depending on the problem or measurement taken. Alternatively, you can enter the circumference of the circular base instead. The altitude of a cone or pyramid is the length of a segment from the vertex point to center of the base inside of the shape, forming a right angle at the base. The slant height of a cone or pyramid is the length of a segment from the vertex point to the base along the outside of the shape.

Let's go through an example where we calculate the length of the slant height of a pyramid. In this example, we are given that the altitude of the pyramid measures 8 inches and each side of the base is 12 inches long. The altitude is the dashed red segment DM and the slant height is the purple segment DY. In this method, you are basically calculating the volume of the cone as if it was a cylinder.

When you calculate the area of the base circle, and multiply it by the height, you are "stacking" the area up until it reaches the height, thus creating a cylinder. And because a cylinder can fit three cones of its matching measurements, you multiply it by one third so that it's the volume of a cone. This provides you with the volume of the cone. With the Pythagorean theorem, use the radius and the height to calculate the slant height of the cone, then multiply the slant height by the radius by pi.

That gives you the lateral area of the cone. To that you add the base area of the cone, which is found by multiplying pi by the square of the radius. The total surface area is found by adding the lateral surface area to the base area. This online calculator will calculate the various properties of a right circular cone given any 2 known variables. The term "circular" clarifies this shape as a pyramid with a circular cross section.

The term "right" means that the vertex of the cone is centered above the base. Using the term "cone" by itself often commonly means a right circular cone. In projective geometry, a cylinder is simply a cone whose apex is at infinity. This is useful in the definition of degenerate conics, which require considering the cylindrical conics. The "base radius" of a circular cone is the radius of its base; often this is simply called the radius of the cone.

The aperture of a right circular cone is the maximum angle between two generatrix lines; if the generatrix makes an angle θ to the axis, the aperture is 2θ. Since the cross sectional areas are also equal, we can employ Cavalieri's principle and state that the volume of the cone equals the volume of the pyramid. We know that the volume of the pyramid is . Since the height is the same in both solids, B must equal πr2 for the cone, making the formula for the volume of a cone . Learn how to compute for the surface area and volume of truncated solids.

Formula 1 Baku 2021 Race Results

On lap 30, the safety car was deployed after Lance Stroll's Aston Martin suffered a left rear tyre blowout on the high-speed pit straight. 15 laps later race leader Verstappen suffered a similar issue as he saw his Red Bull slam the wall at a high speed, resulting in the race being red-flagged with just four laps remaining. The red flag meant that when racing resumed a standing start would take place with Perez leading the pack. With the tyre failures on the rear for both Stroll and Verstappen, Pirelli lodged an investigation over the durability of the selected tyre compounds, their initial findings suggesting the tyre problems were linked to debris.

Race director Masi is expected to reiterate the importance of yellow flag conditions to drivers prior to the 2021 French Grand Prix after the complaints lodged by McLaren during the race. Drivers, including Leclerc, said they would query the decision to delay the deployment of the safety car following Verstappen's crash late in the race. Masi defended his decision to restart the race with just two laps remaining from a standing start, saying there was no reason not to resume racing. Race winner Sergio Pérez revealed his car was close to retiring as he was managing an unspecified issue. Leclerc benefitted a slipstream from Hamilton to set the fastest time early on, while Hamilton got to second fastest from a tow from Bottas, who could only wind up 10th. Both Verstappen and Perez were only able to clock in third and seventh fastest respectively, with Gasly the best of the rest with 4th fastest.

The session was red-flagged for the fourth time when Tsunoda first crashed into Turn 3 with Leclerc's team-mate Sainz, who was following behind, spun into the run-off and damaged his front wing. Leclerc thus secured his 9th career pole, with Hamilton starting alongside him after Mercedes' slow performance on Friday practice. The number of red flags deployed thus equaled the 2016 Hungarian Grand Prix for the most red flags deployed in a qualifying session. Norris, who qualified 6th, was given a three-place grid penalty for a red flag infringement during Q1, therefore demoted to 9th. The order settled over the next fifteen laps with Hamilton unsuccessfully trying to pass Pérez for second place.

Stroll's stricken car had ended up on the pit lane entry and the pit lane was closed until it had been cleared. When the pit lane opened, the field had been brought together behind the safety car and none of the front runners elected to make a pit stop. The only ones who took a fresh set of tyres during the safety car period were Fernando Alonso, Antonio Giovinazzi, George Russell, and Nikita Mazepin. In lap 47 race leader Verstappen also got a puncture on the main straight and also crashed into the barrier on maximum speed with only 4 laps to go.

The safety car deployed for the second time to recover the Red Bull and the debris on the track which resulted in a red flag. The drama dutifully returned on the street circuit of Azerbaijan's capital, with a joint-record four red flags brought out during Saturday's qualifying session. Ferrari's Charles Leclerc managed to grasp pole position for the second race in a row but failed to keep it beyond lap two, when he was overtaken by Lewis Hamilton.

After that the Monegasque went backwards down the order but recovered to fourth. The race was red-flagged, allowing the track to be cleared and all cars were able to change tyres. From a standing start, for the final two laps, Perez was beaten off the startline by Hamilton, but the seven-time world champion locked-up and went straight on at Turn 1, dropping to the tail of the field.

After qualifying Lando Norris said he was left "gutted" after he was handed a three-place grid penalty as well as three-penalty points on his FIA Super Licence for failing to correctly follow the red flag procedures. Valtteri Bottas was mystified with his qualifying performance after finishing down in tenth, eight positions behind teammate Hamilton, saying "something is wrong" with his car. Leclerc led at the start, with Hamilton taking the lead by slipstreaming Leclerc a few laps later. A delayed pit stop release for Hamilton relegated him to behind the Red Bulls, with Verstappen and Sergio Pérez leading. The Safety Car was deployed after Lance Stroll had a tire failure and wrecked on the main straight. Then, with five laps from the finish, Verstappen suffered the same fate as Stroll, causing the red flag.

At the restart, Hamilton locked up into Turn 1, dropping down the order while Perez was left to cruise to his second career victory. Sebastian Vettel gave Aston Martin their first podium in second, with AlphaTauri's Pierre Gasly in third. All drivers could change tyres and a standing restart was called with two racing laps, with Sergio restarting from pole position, Pierre fourth and Yuki seventh. Red Bull's Verstappen was cruising to victory with three laps remaining when his left-rear tyre blew, in similar fashion to Lance Stroll's earlier incident which caused his Aston Martin to crash violently. Both championship contenders, Lewis Hamilton and Max Verstappen, experienced problems during the 51-lap race; Verstappen retired due to a high-speed tyre blowout, while Hamilton made a severe error at the resultant restart.

Their troubles cleared the way for Sergio Pérez, Verstappen's teammate, to win his second Grand Prix, following his victory at the 2020 Sakhir Grand Prix. Sebastian Vettel took second place for his first podium with Aston Martin, while Pierre Gasly claimed third place for AlphaTauri. After the race, tyre supplier Pirelli launched an investigation into the tyre failures which ended the races of Verstappen and Lance Stroll. Verstappen took the lead after a crucial sequence of pit stops, Hamilton starting that sequence on Lap 12 with a slow switch for hards thanks to traffic in the pit lane. Verstappen pitted a lap later and emerged first, followed by Perez who split the championship rivals.

And the Dutchman seemed to have victory in the bag, mastering a Lap 35 Safety Car restart after Lance Stroll's terrifying accident, when the Aston Martin driver's left-rear tyre appeared to gave way on the pit straight. A red flag misdemeanour in qualifying earned him a grid penalty, but he kept his cool to move forwards in the race when others around him got stuck. Fifth place was a solid return for a hard day's work and extended his points-scoring run to 11 races.

He's the only driver to have scored in every grand prix this season. I feel very sorry for Max because he deserved the win and a 1-2 for the Team would've been very enjoyable. We were basically flat out from the very first lap and I had Lewis behind pushing me so I couldn't breathe, it was very challenging but we kept our focus. Everything worked perfectly today apart from the restart at the end where I just had no grip. I thought I cannot lose this race two laps from the flag so I broke as late as I could into Turn 1 and then I saw Lewis locking up and go straight on into the runoff.

We have to enjoy today, our pace was great and we have a very good race car. We are working flat out and giving our best every week, it's only race six and there's more to come from me, the relationship with Max and the Team is great and there's still a long way to go in this championship. Perez and Vettel made good starts at the start of the race, gaining positions in the chain of racing cars. Leclerc, despite starting from pole position, was overtaken by Hamilton before DRS was enabled due to avoiding a tree branch at an earlier part of the circuit. Ocon suffered a power unit failure on the fourth lap, becoming the first retirement of the race. As Hamilton pitted, his pit exit was delayed to avoid an unsafe release upon Gasly.

Verstappen and Perez later stopped, the latter's having a slower stop but still got ahead of Hamilton. The Red Bulls' stops meant that Vettel was promoted into the lead in Aston Martin. Verstappen began to pull away as Hamilton stayed close within Perez. The Jeddah Corniche Circuit is a street circuit in Jeddah, the second largest city in Saudi Arabia.

Jeddah was the first to host the Saudi Arabia Grand Prix, which was held on 5th December 2021. The race was a spectacle to watch because of the multiple red and yellow flags, crashes and time penalties. The new circuit was designed by Carsten Tilke, the son of Hermann Tilke who has many Formula 1 circuits to his name. Jeddah Corniche Circuit became, after the Grands Prix of Singapore and Bahrain, the third full evening race on the F1 calendar. The circuit was announced as the fastest and longest street circuit on the Formula 1 schedule. Max Verstappen has said that he finds it a very cool track, but also that the designer is 'crazy' – because of the many blind corners and speed of the track.

The length of the track is 6.175 kilometres on which the drivers race 50 laps. Meanwhile Stroll was by the accident ahead and drove into the side of Leclerc. After a safety car, teams were told there would be a standing start from the grid, but just beforehand all the drivers except leader Hamilton dived into the pits for slick tyres, as the track was drying. Lewis Hamilton came unstuck in last year's gripping F1 title race because he was 'fighting fire' against Max Verstappen , says former driver David Coulthard .

Verstappen got the better of Hamilton in a historic battle for the 2021 championship, pipping his arch-rival to the crown after a controversial finale out in Abu Dhabi. The pair had already clashed on several occasions throughout the season, including when Verstappen was penalised for a collision with his title nemesis at the Saudi Arabian Grand Prix. And the Dutchman eventually romped home to glory in contentious fashion, passing Hamilton on the final lap despite a late safety car emerging after a Nicholas Latifi crash. Penalised three grid places to P9 for a red-flag violation in qualifying, Lando Norris fell to P11 at the start.

He was under pressure from McLaren to keep the pace up with team mate Daniel Ricciardo just behind and Valtteri Bottas ahead, the Mercedes driver having endured a difficult qualifying session. Norris undercut Bottas on Lap 8 and rallied on the late Safety Car restart to finish a brilliant fifth, even threatening Gasly for the final podium place on Lap 50. Everything came to a standstill, the drivers stopping in the pits for 35 minutes to aid a lengthy clean-up.

And the race would restart, drivers starting from their new slots on the grid, on Lap 50 of 51, all having changed tyres. Crucially, Vettel had a brand new set of softs in the bank. Perez would lead Hamilton, Vettel, Gasly, and Leclerc in P5 – whose Lap 10 undercut attempt on Gasly, starting P4, had not worked. Arriving in Baku as championship leader for the first time, the Red Bull Racing driver was on the hunt for a second consecutive win this season and a first podium of any kind in Baku. For much of this race, it appeared a 13th career win would be the reward on the occasion of Verstappen's 125th start. Another crucial blow dealt to Hamilton's title hopes, surely?

He inherited the lead when his teammate Verstappen's left rear tyre shredded triggering a high-speed crash in the straight as he was set to cash in on his second straight win and third of the season. Verstappen dominated the race after taking the lead from title rival Lewis Hamilton during the pitstops. The Dutchman looked on course for a certain win until his left-rear tyre failed with five laps ago and he suffered a massive shunt on Baku's long start-finish straight.

Stroll ran even longer on his first stint than team-mate Vettel after crashing out of qualifying, and held fourth on lap 31 when he crashed heavily on the start/finish straight due to a left-rear blowout. That caused a safety car, but as the pits were closed – due to Stroll's car blocking the pit entry – it only served to close the pack up rather than switch the order. Then another bombshell moment struck on Lap 47 when Verstappen's left rear tyre also appeared to fail and another high-speed accident on the main straight followed. The race leader was unhurt, but out, leaving Red Bull without a first one-two in Baku and Verstappen without a chance to extend his championship lead. What seemed a comfortable victory was dashed in a milli-second. Vettel managed a brilliant pass on former team mate Leclerc at Turn 1 on the restart, the Monegasque locking up both front tyres in defence of his position and almost careering into Gasly.

The four-time champion then took P4 off Gasly a lap later on the main straight, leaving the AlphaTauri driver to exclaim "That's not possible! That was until Verstappen himself, comfortably in the lead on Lap 47, spun and crashed after an apparent tyre issue of his own. Unhurt, but shaken, his crash triggered the Safety Car, which turned into a red flag that suspended the race on Lap 48. The race resumed with a standing start 35 minutes later on Lap 50, giving us two laps of flat-out action, the field all having switched tyres during the stoppage. Despite the chaotic Saturday, with two sprint races full of safety cars and yellow flags, it was nice and quiet on the track.

Apart from a safety car after the opening lap and some yellow flags because of drivers who had overshot, it stayed clean, without too many problems. The next race in F2 will be at Silverstone, in just over a month. A chaotic race like today's is busy and demanding for the engineers. Of course, we had planned for various possible scenarios, working with the AlphaTauri engineers before the weekend and were well prepared and Pierre made the most of the opportunity to get on the podium once again. Apart from a mistake in qualifying Yuki also performed well this weekend, doing a decent job and scoring points.

It was his first time in Baku and he made progress through each session. He had some tough race weekends before this one and has worked very hard to improve. Scuderia AlphaTauri Honda is now fifth in the Constructors' championship but it is very close and there is still a long way to go. We have a good chassis and our PU is also performing well, so if we can keep having decent race weekends the results will follow, hopefully producing more podium finishes for Scuderia AlphaTauri Honda.

Pierre followed suit two laps later - with both drivers switching to hard tyres - before Max also stopped on lap 12. During this incident, Latifi received a 10-second stop-go penalty for failing to use the pit lane during the incident. Verstappen complained of having worn tyres with five laps to go, but he couldn't pit without losing second place to Ocon.

Hamilton nursed his own car home to take the win, with Verstappen 7sec behind – his time penalty making no difference to the order. Completing the excitement, Bottas passed Ocon metres before the chequered flag to complete the podium. Perez inherited the lead when Verstappen's left rear tyre shredded triggering a high-speed crash in the straight as he was set to collect his second consecutive win and third of the season. With the Azerbaijan Grand Prix practice sessions having been hit by a few incidents, Saturday's qualifying session was stopped four times with red flags as a number of drivers hit trouble. Perez vaulted into third in the championship with the win, while Verstappen maintained his lead in the driver standings.

The win also saw Red Bull Racing Honda's lead in the constructors championship swell to 26 points after six races. Gasly's podium moved him to eighth in the standings while Tsunoda moved up to 14th with his effort. The teams will have next week off before heading to the Paul Ricard circuit for the June 20 French Grand Prix. The first 45 laps were a tour de force for Honda as all four Honda-powered cars were entrenched in the top eight, led by Max Verstappen, who had the field covered after taking the lead after a quick Lap 13 pit stop. Undaunted when his six-second lead was erased on Lap 31 due to a Lance Stroll crash, he quickly put five seconds between himself, Perez and Hamilton while setting the fastest laps of the race.

The weather was a lot cooler on racedays than previous 2 days. Red Bull driver Sergio Perez had a good first lap and won 2 places to cross the start the second lap as 4th. Lance Stroll was the only one who started on the hard tyres and the Canadian even won 4 positions in the first lap against his rivals who started on the much quicker soft tyres. With both title rivals failing to score, the top two positions remained on the top of the driver standings, Hamilton ending his 54-race streak of finishing in the points in every race entered and started. Pérez' victory saw him move up to third in the standings, with Leclerc's fourth-place finish pushing both Norris and Bottas down the order.

Vettel and Gasly also moved up the order following their surprise podium finishes, pushing down Ricciardo. Raikkonen managed to regain his points following his penalty at Imola. In all, the bottom of the drivers' standings had a major shake up following the incident-filled race. The first race will be held at the Bahrain International Circuit, in the village of Sakhir. The circuit has been on the racing calendar since 2004 and will remain on the F1 programme until 2029. In the desert, the drivers complete 57 laps of the 5.412 km long track.

Formula 1 Race 2021 Results As temperatures can reach 35 degrees in March, the race has been run after sunset since 2014 where floodlights are used to illuminate the track. Grosjean suffered a massive crash in 2020 that almost cost him his life. During this crash, Formula 1 safety was again put to the test and the halo, introduced in 2018, probably saved his life.

Sadly for Bottas, a puncture on lap 33 dropped him out of the race from third position. Both Williams cars later suffered punctures, though Perez had pitted to avoid the same fate to finish fourth. The final podium was Hamilton, Verstappen and then Alonso, in a brilliant drive for Alpine. Norris led for much of the race, and regained the advantage shortly after a late stop for a set of fresh rubber. Hamilton earned the 100th pole position of his career in Barcelona, but duly gave up first position on the first corner of the grand prix, having no option but to sacrifice the spot to an aggressive move by Max Verstappen.